图卷积神经网络
# 图卷积神经网络
# 一、背景
图卷积神经网络(Graph Convolutional Network, GCN),现实中更多重要的数据集都是用图的形式存储的,例如知识图谱,社交网络、通信网络、蛋白质分子结构等等,在图网络领域的地位如同卷积操作在图像处理里的地位一样重要。
图卷积神经网络与传统的网络模型LSTM和CNN等所处理的数据类型有所不同。LSTM和CNN只能用于网格化结构的数据,而图卷积神经网络能够处理具有广义拓扑图结构即邻接矩阵的数据,并深入发掘其特征和规律。
# 二、介绍
对于具有拓扑结构的图数据,可以按照用于网格化结构数据的卷积的思想来定义图卷积。将每个节点的邻居节点的特征(D_^-1/2)*A_*(D_^-1/2)*H传播到该节点,再进行加权,就可以得到该点的聚合特征值。
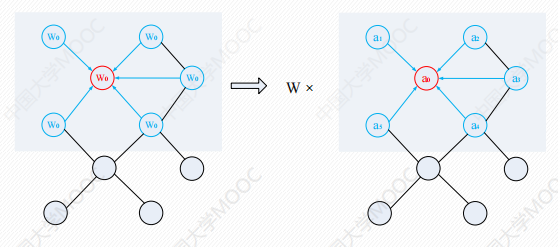
公式如下:
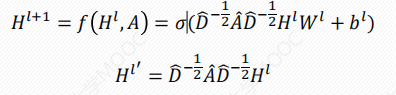
显然,Hl+1的维度和W、B有关。
其中:
- A:邻接矩阵、A_=A+I
- I:单位阵
- D:
A_的对角节点度矩阵(出度) - W:第l层的参数矩阵
- b:第l层的偏置向量
- H:特征矩阵
- H':含有拓扑信息的特征矩阵
- σ:激活函数
# 三、图卷积神经网络vs卷积神经网络
# 3.1 共同点(相同之处)
| 方面 | 内容 |
|---|---|
| 神经网络结构 | 都属于深度神经网络,使用多层网络学习特征表示。 |
| 局部连接思想 | 都强调局部连接的特性:CNN在图像的局部像素上卷积,GCN在图节点的邻居上卷积。 |
| 参数共享 | 卷积核参数在不同位置共享(CNN 是空间共享,GCN 是邻居共享)。 |
| 目标一致 | 都试图从原始数据中提取高级表示(features)用于分类、回归等任务。 |
| 可以端到端训练 | 都可以通过反向传播进行端到端学习。 |
# 3.2 不同点(本质区别)
| 方面 | CNN(卷积神经网络) | GCN(图卷积神经网络) |
|---|---|---|
| 输入数据结构 | 规则的欧几里得结构(如图像,2D 网格) | 非欧几里得结构(如社交网络、知识图谱、分子结构) |
| 卷积操作 | 使用传统的滑动窗口卷积核对固定邻域操作 | 使用图邻接矩阵加权求和邻居信息 |
| 邻域定义 | 图像的局部像素块,邻居是固定的(如 | 图中节点的邻接点,邻居数量不固定 |
| 核心数学工具 | 卷积核、傅里叶变换、矩阵乘法 | 图拉普拉斯算子、邻接矩阵、谱图理论 |
| 应用领域 | 图像识别、视频分析、语音处理等 | 社交推荐、知识图谱推理、蛋白质结构建模、交通预测等 |
| 空间 vs. 图空间 | 在二维空间或序列中卷积 | 在图结构中对节点的邻居进行特征聚合 |
# 3.3 理解
假设你有一个“猫”的图片:
- CNN:会用一个卷积核滑过整张图片提取边缘、纹理等特征。
- GCN:如果“猫”是知识图谱中的一个节点,它会根据与“猫”相连的其他概念(如“动物”、“毛发”、“宠物”)来聚合邻居特征,学习“猫”的表示。
# 四、用Numpy实现图卷积
import numpy as np
from math import sqrt
from functools import reduce
A = np.matrix([
[0,1,0,0],
[0,0,1,1],
[0,1,0,0],
[1,0,1,0],
], dtype=float)
H = np.matrix(
[[i,-i] for i in range(A.shape[0])],
dtype=float
)
I = np.matrix(np.eye(A.shape[0]))
A_ = A + I
D_ = np.array(np.sum(A_, axis=0))
# 对角线
D_sqrt = np.diag([sqrt(i) for i in D_[0]])
D_sqrt_inv = np.linalg.inv(D_sqrt)
W = np.matrix([
[1, -1, 2],
[-1, 1, 3]
])
b = np.matrix([
[1],
[0],
[1],
[0]
])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def getDot(A,B):
return np.dot(A,B)
def relu(x):
return np.where(x>=0, x, 0)
# 累乘
H1 =relu(reduce(getDot,[D_sqrt_inv,A_,D_sqrt_inv,H,W]) + b)
H1
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
array([[1.81649658, 0.18350342, 0.59175171],
[4.44948974, 0. , 0. ],
[3. , 0. , 0. ],
[4.63299316, 0. , 0. ]])
