本文是由笔者总结的笔记,来源自北大余肇飞老师:【20220112【脉络分明:脉冲神经网络及其应用】余肇飞:脉冲神经网络学习理论与方法】 https://www.bilibili.com/video/BV1uT4y127Zr/?share_source=copy_web&vd_source=11da79c1d1fa9faeb59d46943aa4fa9e
# RSNN
RSNN(Recurrent Spiking Neural Network,循环脉冲神经网络)是一类结合了生物神经元脉冲特性SNN和循环结构RNN的神经网络,广泛用于处理时间序列、语音识别、脑机接口等任务。
# 脉冲神经元模型
# 前置知识
 |  |
|---|
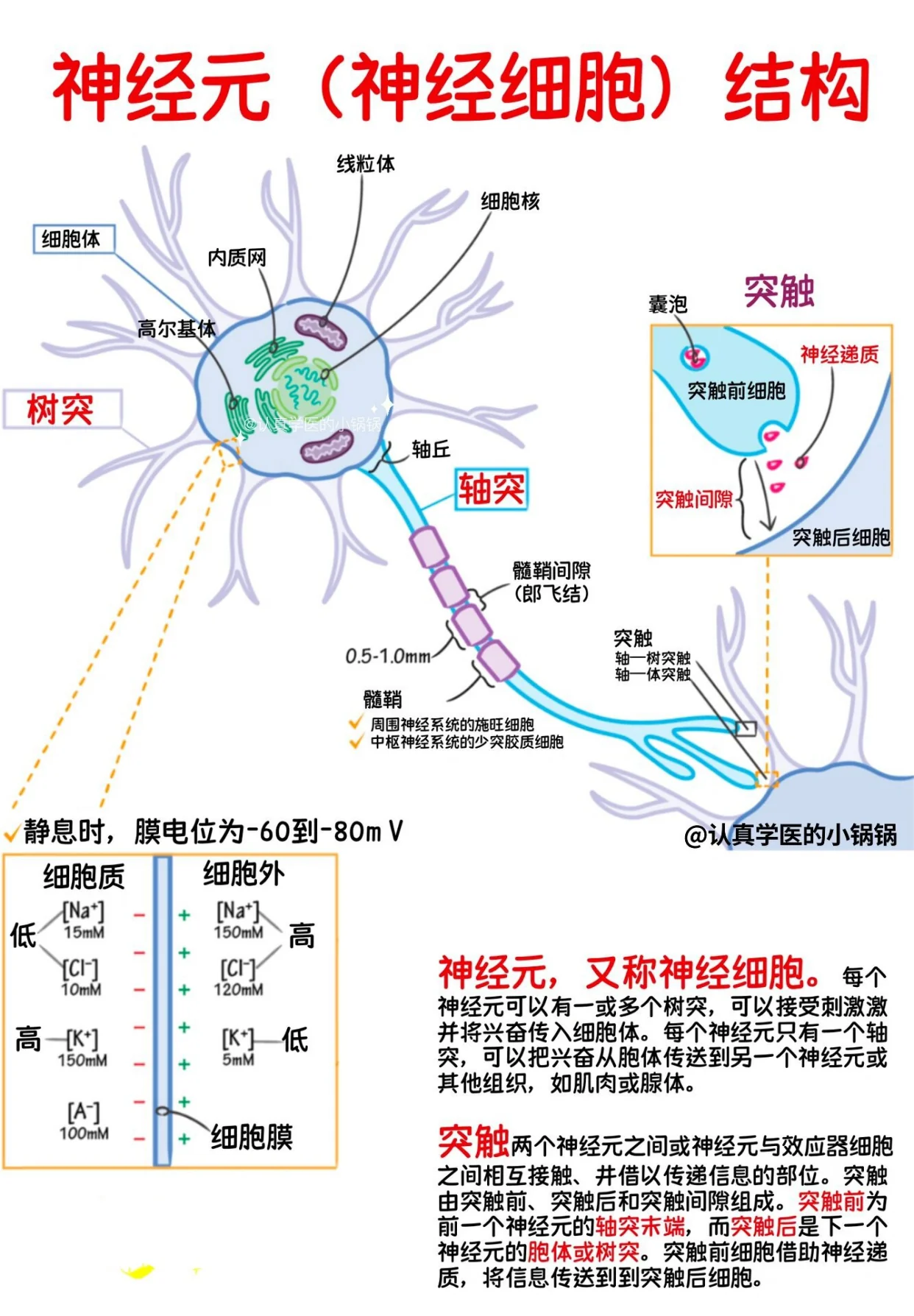
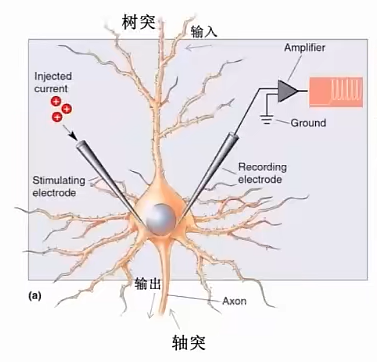
脉冲神经元主要包含胞体、树突和轴突。
树突:信息传来的通路
胞体:类似CPU,信息传来->充电->达阈值->放电
轴突:传给其他神经元的通路
生物学角度:
- 信号接收阶段
树突接收来自其他神经元的神经递质 神经递质与受体结合,引起离子通道开放 产生局部电位变化(兴奋性或抑制性突触后电位)
- 信号整合阶段
多个突触信号在胞体汇集 进行时间总和与空间总和 在轴突起始段(轴丘)判断是否达到阈值(约-55mV)
- 动作电位产生
达到阈值后,钠离子通道大量开放 钠离子内流,膜电位迅速上升至+30mV(去极化) 钠通道失活,钾通道开放 钾离子外流,膜电位恢复(复极化)
- 信号传导阶段
动作电位沿轴突传播 有髓鞘:跳跃式传导(郎飞结之间) 无髓鞘:连续传导 传导速度:1-120米/秒
- 突触传递阶段
动作电位到达轴突末梢 钙离子通道开放,钙离子内流 触发突触小泡与膜融合 释放神经递质到突触间隙(20-40纳米)
- 信号终止
神经递质被分解酶降解 或被突触前膜重吸收 或扩散离开突触间隙
其中,神经元信息传递主要通过脉冲。
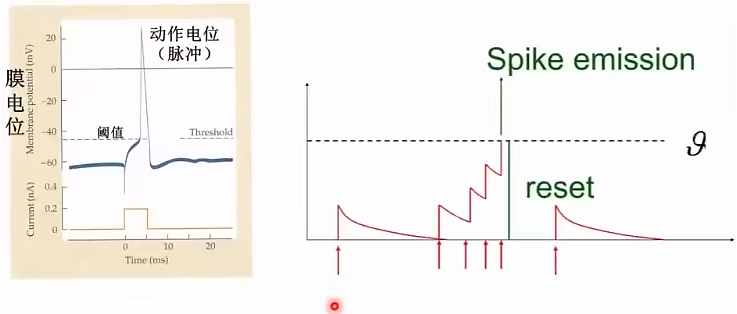
前一个神经元发放一个脉冲,就会传给下一个神经元,电压累积。若发来多个脉冲**,电压累积到阈值,就发放一个脉冲给下一个神经元**。
# 数学模型描述
# 微分方程
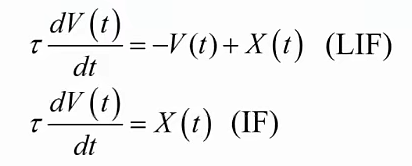
# 仿真离散的差分方程
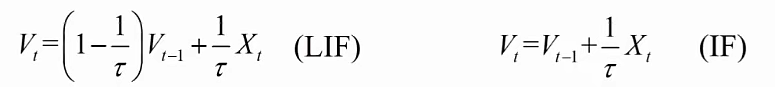
# 流程
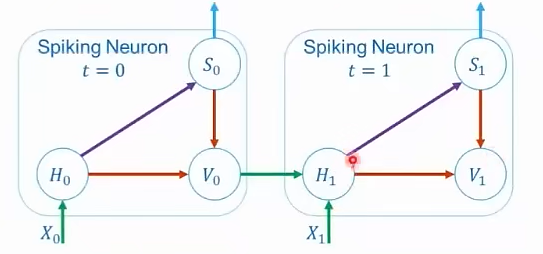
: t时刻的输入 : t时刻充电后的膜电位 : t时刻发放的脉冲 : t时刻发放脉冲后的膜电位
- 充电
对LIF模型 对IF模型
其中:
- τ(tau)是一个关键的时间常数,代表膜电位衰减的快慢。
- τ 大:神经元“记性好”,膜电位V衰减得慢,信息保留时间更长。
- τ 小:神经元“记性差”,膜电位很快就回到初始状态。
- Ht表示神经元动力学后的膜电位。
- Xt表示额外输入
放电
电压累积到阈值,St置为1。
重置
硬重置
膜电位直接被重置为Vreset
软重置
膜电位减少Vth
Vt表示在时间步t触发锋电位后的膜电位。
# 学习方法
# 梯度替代法
由于BP算法训练,放电函数是单位阶跃函数,不可微,在x=0处导数无穷大。于是在反向传播时,用一个新函数替代原放电函数。前向传播保持不变。
前向传播:
后向传播:
如
具体流程(surrogate gradient 方法)
- 前向传播:
- 更新膜电位
- 判断是否发放脉冲
- 记录 spike 时间序列
- 计算 loss(比如输出 spike 序列和目标序列的 MSE)
- 反向传播:
- 展开所有时间步(BPTT)
- 用 surrogate gradient 估计每一层的脉冲函数的导数
- 更新权重
# 例子(From Claude)
# 代码
我来手写一个简单的循环脉冲神经网络(RSNN)例子,帮你理解各个组件的作用。
import numpy as np
import matplotlib.pyplot as plt
# 梯度替代函数(用于反向传播)
def surrogate_gradient(v, threshold=1.0, beta=1.0):
"""
使用sigmoid函数的导数作为脉冲函数的梯度替代
v: 膜电位
threshold: 阈值
beta: 控制梯度的尖锐程度
"""
return beta * np.exp(-beta * np.abs(v - threshold)) / 2.0
class SimpleRSNN:
def __init__(self, input_size=2, hidden_size=4, output_size=1):
"""
输入层: 2个神经元(比如表示两个传感器的脉冲序列)
隐藏层: 4个神经元(循环连接,有记忆)
输出层: 1个神经元(二分类输出)
"""
# 初始化权重
self.W_in = np.random.randn(hidden_size, input_size) * 0.5 # 输入到隐藏层
self.W_rec = np.random.randn(hidden_size, hidden_size) * 0.3 # 循环连接
self.W_out = np.random.randn(output_size, hidden_size) * 0.5 # 隐藏到输出
# LIF神经元参数
self.tau_m = 10.0 # 膜时间常数
self.threshold = 1.0 # 脉冲阈值
self.dt = 1.0 # 时间步长
self.decay = np.exp(-self.dt / self.tau_m) # 膜电位衰减因子
def forward(self, x_sequence):
"""
前向传播
x_sequence: 输入脉冲序列 [时间步数, 输入维度]
"""
T = x_sequence.shape[0] # 时间步数
batch_size = 1
# 记录各层的状态(用于反向传播)
self.v_hidden = np.zeros((T+1, self.hidden_size)) # 隐藏层膜电位
self.s_hidden = np.zeros((T, self.hidden_size)) # 隐藏层脉冲
self.v_out = np.zeros((T+1, self.output_size)) # 输出层膜电位
self.s_out = np.zeros((T, self.output_size)) # 输出层脉冲
# 逐时间步计算
for t in range(T):
# 1. 隐藏层:接收输入脉冲和循环脉冲
input_current = np.dot(self.W_in, x_sequence[t])
if t > 0:
recurrent_current = np.dot(self.W_rec, self.s_hidden[t-1])
else:
recurrent_current = 0
# 2. 更新隐藏层膜电位(LIF模型)
self.v_hidden[t+1] = self.decay * self.v_hidden[t] + input_current + recurrent_current
# 3. 产生脉冲(如果膜电位超过阈值)
self.s_hidden[t] = (self.v_hidden[t+1] >= self.threshold).astype(float)
# 重置发放脉冲的神经元
self.v_hidden[t+1] = self.v_hidden[t+1] * (1 - self.s_hidden[t])
# 4. 输出层:接收隐藏层脉冲
output_current = np.dot(self.W_out, self.s_hidden[t])
self.v_out[t+1] = self.decay * self.v_out[t] + output_current
self.s_out[t] = (self.v_out[t+1] >= self.threshold).astype(float)
self.v_out[t+1] = self.v_out[t+1] * (1 - self.s_out[t])
# 返回输出脉冲的发放率(作为分类的依据)
return np.mean(self.s_out)
def backward(self, x_sequence, target, learning_rate=0.01):
"""
反向传播(使用梯度替代法)
target: 目标输出(0或1)
"""
T = x_sequence.shape[0]
output = np.mean(self.s_out)
loss = (output - target) ** 2
# 初始化梯度
dW_in = np.zeros_like(self.W_in)
dW_rec = np.zeros_like(self.W_rec)
dW_out = np.zeros_like(self.W_out)
# 输出层的误差
dL_dout = 2 * (output - target) / T
# 反向传播通过时间(BPTT)
dv_out_next = np.zeros(self.output_size)
dv_hidden_next = np.zeros(self.hidden_size)
for t in reversed(range(T)):
# 输出层梯度
surrogate_grad_out = surrogate_gradient(self.v_out[t+1], self.threshold)
ds_out = dL_dout * surrogate_grad_out
dv_out = ds_out + self.decay * dv_out_next
dv_out_next = dv_out * (1 - self.s_out[t])
# 权重梯度 W_out
dW_out += np.outer(dv_out, self.s_hidden[t])
# 隐藏层梯度
dh = np.dot(self.W_out.T, dv_out)
surrogate_grad_hidden = surrogate_gradient(self.v_hidden[t+1], self.threshold)
ds_hidden = dh * surrogate_grad_hidden + dv_hidden_next
dv_hidden = ds_hidden + self.decay * dv_hidden_next
# 权重梯度 W_in
dW_in += np.outer(dv_hidden, x_sequence[t])
# 权重梯度 W_rec(循环连接)
if t > 0:
dW_rec += np.outer(dv_hidden, self.s_hidden[t-1])
# 传递梯度到下一时间步
if t > 0:
dv_hidden_next = np.dot(self.W_rec.T, ds_hidden) * (1 - self.s_hidden[t-1])
else:
dv_hidden_next = np.zeros(self.hidden_size)
# 更新权重
self.W_in -= learning_rate * dW_in
self.W_rec -= learning_rate * dW_rec
self.W_out -= learning_rate * dW_out
return loss
# 使用例子:识别脉冲序列模式
def create_sample_data():
"""
创建两类脉冲序列:
类别0: 低频率脉冲
类别1: 高频率脉冲
"""
T = 20 # 时间步
# 类别0:稀疏脉冲
x0 = np.random.rand(T, 2) < 0.1 # 10%概率发放脉冲
y0 = 0
# 类别1:密集脉冲
x1 = np.random.rand(T, 2) < 0.5 # 50%概率发放脉冲
y1 = 1
return [(x0.astype(float), y0), (x1.astype(float), y1)]
# 训练网络
rsnn = SimpleRSNN(input_size=2, hidden_size=4, output_size=1)
# 生成训练数据
train_data = []
for _ in range(100):
train_data.extend(create_sample_data())
# 训练循环
losses = []
for epoch in range(50):
epoch_loss = 0
np.random.shuffle(train_data)
for x, y in train_data:
output = rsnn.forward(x)
loss = rsnn.backward(x, y, learning_rate=0.01)
epoch_loss += loss
avg_loss = epoch_loss / len(train_data)
losses.append(avg_loss)
if epoch % 10 == 0:
print(f"Epoch {epoch}, Loss: {avg_loss:.4f}")
# 可视化训练过程
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('RSNN Training Loss')
plt.show()
# 测试网络
print("\n测试结果:")
test_data = create_sample_data() * 5
correct = 0
for x, y in test_data:
output = rsnn.forward(x)
prediction = 1 if output > 0.5 else 0
correct += (prediction == y)
print(f"真实类别: {y}, 预测输出: {output:.3f}, 预测类别: {prediction}")
print(f"\n准确率: {correct/len(test_data)*100:.1f}%")
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
让我详细解释各个部分:
# 1. 输入是什么?
# 输入是脉冲序列(0或1),形状为 [时间步数, 输入维度]
# 例如:20个时间步,2个输入通道
x_sequence = np.array([
[1, 0], # t=0: 第一个神经元发放,第二个不发放
[0, 1], # t=1: 第一个不发放,第二个发放
[0, 0], # t=2: 都不发放
...
])
2
3
4
5
6
7
8
# 2. 权重是什么?
- W_in: 输入层到隐藏层的连接权重(4×2矩阵)
- W_rec: 隐藏层的循环连接权重(4×4矩阵),让网络有记忆
- W_out: 隐藏层到输出层的权重(1×4矩阵)
# 3. 中间层进行了什么?
隐藏层实现了LIF(Leaky Integrate-and-Fire)神经元模型:
- 积分:收集输入电流,膜电位逐渐上升
- 泄漏:膜电位会自然衰减
- 发放:当膜电位超过阈值时,发放脉冲
- 循环:接收自己之前时刻的输出,形成记忆
# 4. 输出是什么?
输出层计算脉冲发放率,用于分类:
- 低发放率(接近0)→ 类别0
- 高发放率(接近1)→ 类别1
# 5. 梯度替代法的作用
脉冲函数是不可微的阶跃函数,无法直接求导。梯度替代法用平滑函数(如sigmoid导数)近似脉冲函数的梯度,使得反向传播成为可能。
这个例子展示了RSNN如何处理时序脉冲数据,通过循环连接保持记忆,并使用梯度替代法进行训练。
