循环神经网络

# 循环神经网络

# 背景

对于普通神经网络，例如多层感知机，其前一个输入和后一个输入完全没有联系，导致在处理时间序列问题时，难以精准刻画时间序列中的时间关系。

为了更好地处理时间序列问题，学者提出了循环神经网络结构（Recurrent Neural Network），最基本的循环神经网络由输入层、一个隐藏层和一个输出层组成。

# RNN 简介

循环神经网络结构（Recurrent Neural Network）

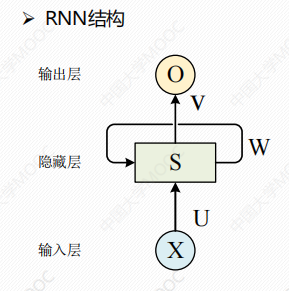
解释：

X：输入层的值
U：输入到隐藏层的权重矩阵
V：隐藏层到输出层的权重矩阵
O：输出层
S：是一个向量，表示隐藏层的值，其不仅仅取决于当前的输入X，还取决于上一时刻隐藏层的值。如果去掉有W的带箭头的连接线，即为普通的全连接神经网络。
W：隐藏层上一时刻的值，作为当前时刻输入的权重矩阵

公式：

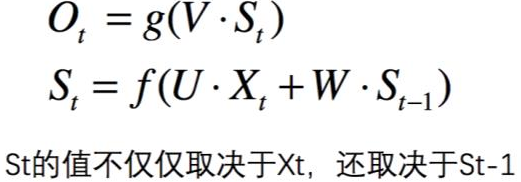
解释：

f即为激活函数

把RNN结构按照时间线展开。（Elman）

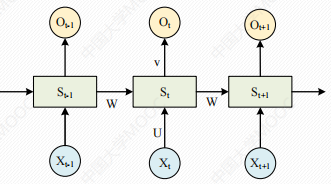
若只要一个输出，不要Ot、Ot-1即可。

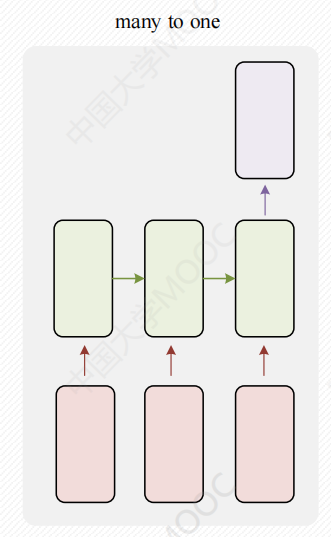
RNN与基础的神经网络最大的不同之处在于同一层内的神经元在不同时刻也建立了全连接，即W与时间有关。

# LSTM

LSTM（Long Short-Term Memory）模型，属于RNN的一种。

循环神经网络图LSTM

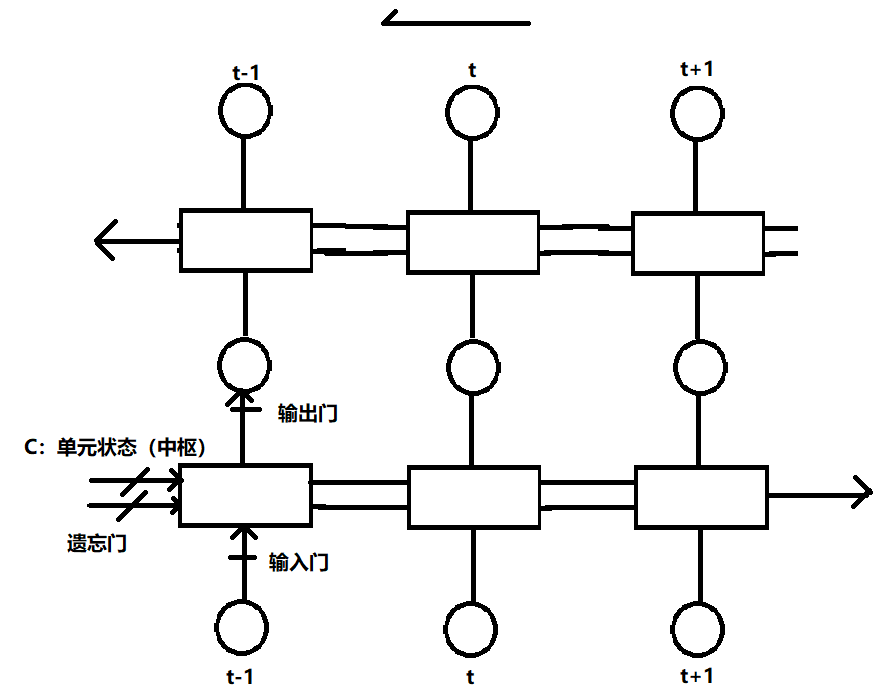
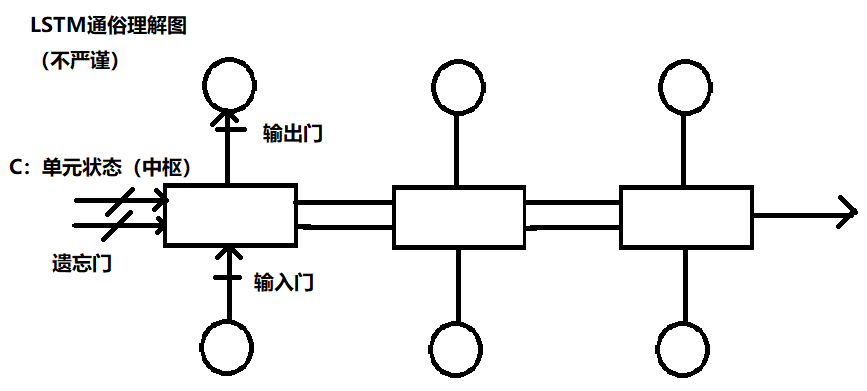
# 与RNN区别

RNN和LSTM最大区别在于分布在隐藏层的神经元结构。

LSTM的记忆单元（Block）更加复杂，LSTM模型中增加了状态𝑐，称为单元状态（cell state），用来保存长期的状态，而LSTM的关键，就是怎样控制长期状态

# LSTM的重复模块

真实图：

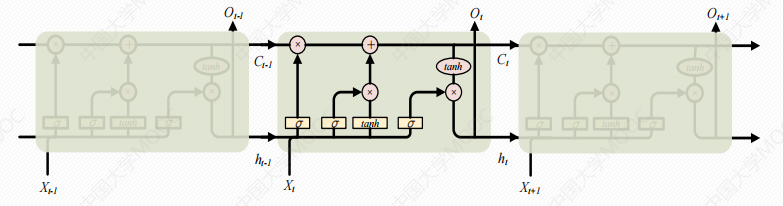
公式：

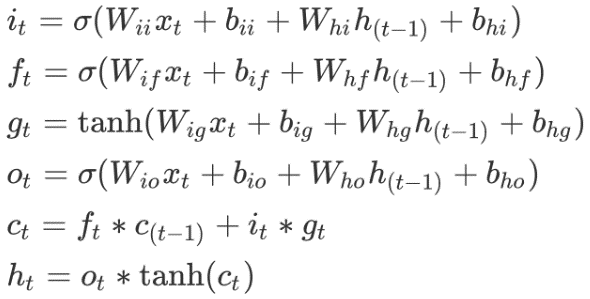
LSTM的核心是单元的状态，单元状态的传递类似于传送带，直接在整个时间链上运行，中间值有一些少量的线性交互，便于保存相关信息。

# 实现

导包

from torch import nn
from torch.autograd import Variable
import torch

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

1
2
3
4
5
6
7

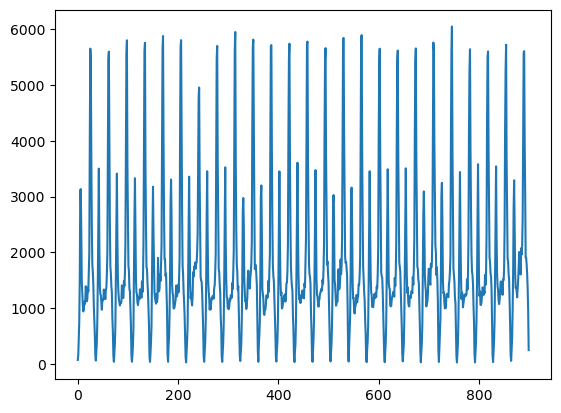
数据展示

file_path = './LSTM.csv'
data = pd.read_csv(file_path)
data.dropna(inplace=True)
plt.plot(data)
plt.show()

1
2
3
4
5

png

数据归一化

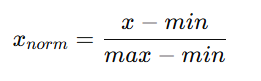
# 归一化 所有数据缩放到 0和1之间
data_ndarray = data.values
data_ndarray = data_ndarray.astype('float32')
max_num = np.max(data_ndarray)
min_num = np.min(data_ndarray)
scalar = max_num - min_num

dataset = list(map(lambda x: (x - min_num)/scalar,data_ndarray))

1
2
3
4
5
6
7
8

初始化训练和测试数据

'''
初始化数据
把前2个时间粒度的客流数据作为输入,把当前时间粒度的客流数据作为输出
返回：测试集、训练集
'''
def create_dataset(data,step=5, train_percent=0.7):
    dataX = []
    dataY = []
    data_len = len(data)
    for i in np.arange(data_len - step):
        split_num = i+step
        dataX.append(data[i:split_num])
        dataY.append(data[split_num])

    # 区分测试、训练集
    dataX_len = len(dataX)
    dataY_len = len(dataY)
    split_index = int(dataX_len * train_percent)
    
    trainX = torch.from_numpy(np.array(dataX[:split_index]).reshape(-1,1,5))
    trainY = torch.from_numpy(np.array(dataY[:split_index]).reshape(-1,1,1))
    testX = torch.from_numpy(np.array(dataX[split_index:]).reshape(-1,1,5))
    testY = torch.from_numpy(np.array(dataY[split_index:]).reshape(-1,1,1))

    return trainX, trainY, testX, testY

trainX, trainY, testX, testY = create_dataset(dataset)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

建立模型

在 nn.Module 内部，有 __call__() 魔法方法。

当你调用一个对象时，Python 会自动触发这个对象的 call 方法。
```
def __call__(self, *input, **kwargs):
    return self.forward(*input, **kwargs)
```
1
2

class LSTM_LINEAR(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super().__init__()
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers)
        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x, _ = self.lstm(x) # (seq, batch, hidden)
        s,b,h = x.shape
        # 降维，匹配linear参数要求
        x = x.view(s*b, h)
        x = self.linear(x) # input:(*, Hin), Hin即 hidden_size
        x = x.view(s,b,-1)
        return x

# 实例化
net = LSTM_LINEAR(5,45)
# 损失
criterion = nn.MSELoss()
# 优化器
optimizer = torch.optim.Adam(net.parameters(), lr=1e-2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

训练

# 训练
for e in range(200):
    out = net(trainX)
    loss = criterion(out, trainY)
    # 梯度清零
    optimizer.zero_grad()
    loss.backward()
    # 更新模型参数
    optimizer.step()
    if e%10==0:
        print(f'epoch: {e}, loss: {loss.item()}')

1
2
3
4
5
6
7
8
9
10
11

epoch: 0, loss: 0.23863691091537476
epoch: 10, loss: 0.04517023265361786
epoch: 20, loss: 0.04236963018774986
epoch: 30, loss: 0.03165356442332268
epoch: 40, loss: 0.02464795857667923
epoch: 50, loss: 0.017756391316652298
epoch: 60, loss: 0.010942698456346989
epoch: 70, loss: 0.0064301323145627975
epoch: 80, loss: 0.004891194868832827
epoch: 90, loss: 0.004182700999081135
epoch: 100, loss: 0.0035117552615702152
epoch: 110, loss: 0.0030126941855996847
epoch: 120, loss: 0.002448414918035269
epoch: 130, loss: 0.0033389576710760593
epoch: 140, loss: 0.0027324846014380455
epoch: 150, loss: 0.0020164402667433023
epoch: 160, loss: 0.0015253744786605239
epoch: 170, loss: 0.001150979078374803
epoch: 180, loss: 0.0025168675929307938
epoch: 190, loss: 0.001205406035296619

测试

# 转为测试模式
net = net.eval()
with torch.no_grad():
    out = net(testX)
    loss = criterion(out, testY)

print(f'sample is test, loss is {loss.item()}')

1
2
3
4
5
6
7

sample is test, loss is 0.001995484111830592

预测并反归一化

# 反归一化
def restore(x):
    return x.view(-1).data.numpy()*scalar +min_num

pre_testX = net(testX)
pre_testX_new = restore(pre_testX) # 预测值
testY_new = restore(testY) # 真实值

1
2
3
4
5
6
7

画图

plt.figure(figsize=(6,4))
plt.plot(pre_testX_new, label='predict')
plt.plot(testY_new, label='real')

plt.show()

1
2
3
4
5

反向传播算法卷积神经网络

Hola，最近还好吗？

Choose mode

循环神经网络

# 循环神经网络

# 背景

# RNN 简介

# LSTM

# 与RNN区别

# LSTM的重复模块

# 实现