优化器模块

# 优化器模块

优化参数的具体机制。工具包：torch.optim

# 使用optimizer

optimizer = optim.Adam(net.parameters(), lr =0.001)
# 单独设置参数 
optimizer = optim.Adam([{'params':model.base.parameters()},{'params':model.regression.parameters(), 'lr': 0.0001}], lr = 0.001)

1
2
3

其中，

net.parameters：所有参数
lr：学习率

# 常见优化器

梯度下降
逐参数适应学习率方法

# 梯度下降法

# 批量梯度下降（batch gradient descent）

通过对所有样本的计算来求解梯度的方向，梯度方差小。

缺点：需要较多的计算资源

# 随机梯度下降（stochastic gradient descent）

每次随机选取一个样本的损失函数来求梯度，训练速度快。

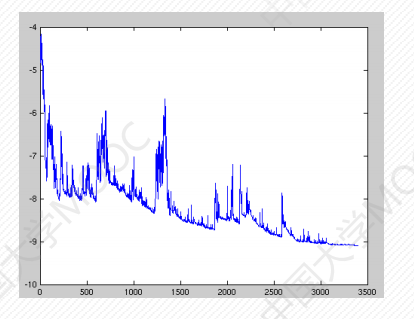
缺点：

方差大，损失震荡严重。
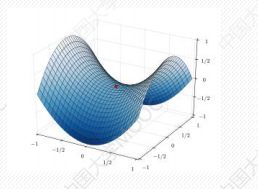
由于鞍点的存在可能导致局部梯度为零，无法继续移动，使得最优解可能仅为局部最优。

# 小批量梯度下降（mini-batch gradient descent）

即把数据分为若干个批，按批量来更新参数。

优点：减少了梯度下降的随机性，也减少了计算量。

缺点：该方法选择一个合适的学习率比较困难；且梯度容易被困在鞍点。

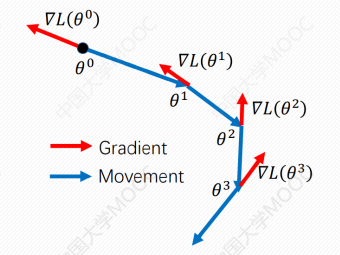
# 动量优化算法（Momentum）

通过使用最近一段时间内的平均梯度来代替当前时刻的随机梯度作为参数更新的方向，从而提高优化速度。

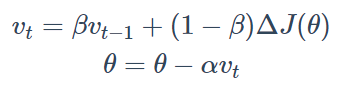
即过去方向+当前方向的加权平均和（惯性）

# 逐参数适应学习率方法

# AdaGrad

基本思想是对每个变量采用不同的学习率。

学习率在一开始比较大，用于快速梯度下降；随着优化过程进行，对于已经下降很多的变量，减缓学习率；对于还没怎么下降的变量，则保持较大的学习率。

更新参数公式：

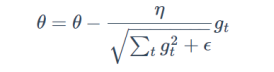
∑gt^2即为梯度的平方累加。

代码：

optimizer = torch.optim.Adagrad(params, lr=0.01, lr_decay=0,weight_decay=0, initial_accumulator_value=0)

缺点：当下降太快，后续调参不好调。

# RMSProp

不像AdaGrad算法那样直接累加平方梯度，而是加了一个衰减系数来控制历史信息的获取多少，即做了一个梯度平方的滑动平均。（类似momentum惯性）

代码：

optimizer = torch.optim.RMSprop(params, lr=0.01, alpha=0.99,eps=1e-08,weight_decay=0,momentum=0,centered=False)

# Adam

即自适应时刻估计方法（Adaptive Moment Estimation）相当于自适应学习率（RMSProp）和动量法（Momentum ）的相结合，能够计算每个参数的自适应学习率，将惯性保持和环境感知这两个优点集于一身。

代码：

optimizer = torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999),eps=1e-08, weight_decay=0)

4激活函数 6训练和测试模块

Hola，最近还好吗？

Choose mode