4 激活函数
# 4 激活函数
torch.nn.functional
# 4.1 简介
在多层神经网络中,上层节点的输出和下层节点的输入之间有一个函数关系。如果这个函数我们设置为非线性函数,深层网络的表达能力将会大幅度提升,几乎可以逼近任何函数,我们把这些非线性函数叫做激活函数。
用途:激活函数的作用就是给网络提供非线性的建模能力。
# 4.2 常用激活函数
# Sigmoid函数
torch.sigmoid()
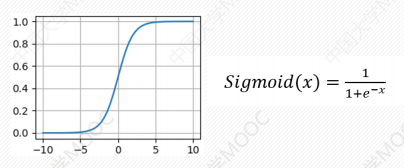
优点:很好地解释了神经元在受到刺激的情况下是否被激活和向后传递的情景。当取值接近0时几乎没有被激活,当取值接近1的时候几乎完全被激活。
缺点:
- 容易出现梯度消失(0.9^100),甚至小概率会出现梯度爆炸(1.1^100)问题
- 含有幂函数,计算机在求解的时候比较耗时
- 输出不是0均值。(经验而言,均值0效果更好)
import torch
x = torch.rand(4)
output = torch.sigmoid(x)
print(output)
2
3
4
5
6
tensor([0.6491, 0.5927, 0.7311, 0.6114])
# Tanh函数
本质是sigmoid函数的一个变形,两者的关系为tanh(x)=2sigmoid(2x)-1 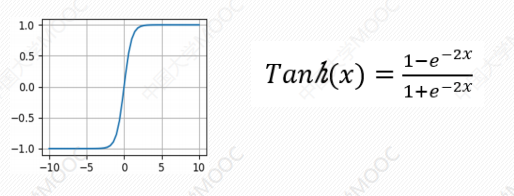
优势:
- 将输出值映射到(-1,1)之间,因此解决了sigmoid函数的非0均值问题
缺点:
- 存在梯度消失和梯度爆炸的问题
- 幂运算也会导致计算耗时久
注意:为了防止饱和情况的发生,在激活函数前可以加一步batch normalization,尽可能的保证神经网络的输入在每一层都具有均值较小的0中心分布
# Relu函数(线性)
Relu是修正线性单元(The Rectified Linear Unit)的简称
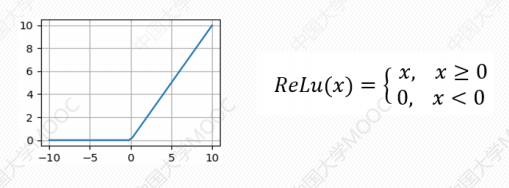
优势:
- 不存在指数运算部分,几乎没有什么计算量
- 具有单侧抑制(负无穷,0)、宽兴奋(0,正无穷)边界的生物学合理性
缺点:有时由于输出反复为0,神经元可能会死亡。
# LeakyRelu函数
解决一部分Relu函数存在的可能杀死神经元的问题(输出加了个斜率)

import torch
x = torch.rand(10)
y = torch.nn.functional.leaky_relu(x,0.03)
print(y)
2
3
4
tensor([0.4088, 0.5671, 0.3428, 0.2739, 0.9709, 0.2129, 0.8612, 0.4952, 0.5532,
0.0693])
# 4.3 nn模块其他常用方法
torch.nn模块,即“Neural Networks(神经网络)”模块,是提供构建神经网络的各种“组件”与“工具”。
这些“组件”包括:
- 神经网络层(linear、conv、lstm…)
- 激活函数(ReLU、Sigmoid、Tanh…)
- 损失函数(MSELoss、CrossEntropyLoss…)
- 正则化层(BatchNorm、Dropout…)
- 容器模块(Sequential、ModuleList、ModuleDict…)
# nn.Linear
nn.Linear(in_features, out_features, bias=True)
| 参数 | 含义 |
|---|---|
in_features | 输入特征的维度 |
out_features | 输出特征的维度 |
bias | 是否加偏置项(默认 True) |
nn.Linear 实现了一个 线性变换(矩阵乘+偏置),输入一个 shape 为 (batch_size, in_features) 的张量,输出 shape 为 (batch_size, out_features),是深度学习中最常用的“全连接层”。
常用于:
- 输入 → 隐藏层映射
- 隐藏层 → 输出层映射
- LSTM / CNN 的输出 → 分类层
# nn.MSELoss
均方误差损失函数
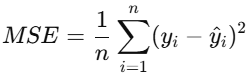
常用
loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()
2
3
4
5
# nn.CrossEntropyLoss
交叉熵损失函数
# 常见 loss:
| Loss 类型 | 场景 | 为啥不能简单做“预测 - 真实” |
|---|---|---|
| MSE(均方误差) | 回归 | 适合连续数值,差的平方反映偏差 |
| BCE(二元交叉熵) | 二分类(概率输出) | 预测 - 标签 不是概率上的“差距” |
| Cross Entropy | 多分类 | 预测是概率分布,标签是分类索引,“误差”必须反映整个分布的差异 |
| KL 散度 | 分布对分布 | 衡量两个分布之间的信息损失,“差值”根本说不清 |
| Hinge Loss | SVM | 要求 margin,而不是概率/值差距 |
# QR
为什么学习规则有那么多种?不就是计算loss 么, 不直接真实和预测之差就行了
# 🔍 类比解释:
想象你在不同场景下扔飞镖:
场景 目标形状 应该怎么评价你扔得准不准? 标准靶子 一个点 距离中心的距离(平方差) 猜硬币正反 二选一 猜中 vs 猜错(二元交叉熵) 猜骰子点数 六选一 哪面概率最高(交叉熵) 猜多个标签 可多选 每个标签独立判断(多标签 BCE) 你不会用“扔远了几米”去评价一个猜正反面的问题,对吧?同理,不同类型的问题 → 不同的误差评价方式(损失函数)。
